

Title2 'Testing if the sample of cholesterol levels in 1952 is statistically different from 200' Īs in our hand calculations, t = 7.72, and we reject H 0 (because p<0.0001 which is < 0.05, our selected α level). Title 'One Sample t-test with proc ttest' Proc ttest data =dixonmassey h0 = 200 alpha = 0.05 The decision rule, "reject if |t| > critical value associated with α" is equivalent to "reject if p critical value associated with α" is equivalent to "reject if p < α." Rather, SAS will provide the p-value, the probability that T is more extreme than observed t. For the hypothesis test, however, it does not compute critical values associated with the given α, and compare the t-statistic to the critical value. SAS uses the stated α for the level of confidence (for example, α=0.05 will result in 95% confidence limits).
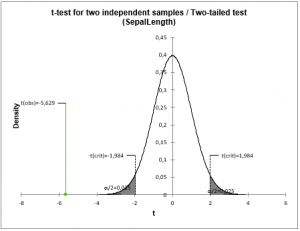
Proc ttest data =name h0 = μ 0 alpha = α When the scaling term is unknown and is replaced by an estimate based on the data, the test. A t-test is the most commonly applied when the test statistic would follow a normal distribution if the value of a scaling term in the test statistic were known. (281.01, 341.29) One Sample t-test Using SAS: The t-test is any statistical hypothesis test in which the test statistic follows a Students t-distribution under the null hypothesis. The 95% confidence limits around the mean are We will test to see if the 1952 population from which the Dixon and Massey sample was gathered is statistically different, on average, from this recommended level. Many doctors recommend having a total cholesterol level below 200 mg/dl. Input Obs chol52 chol62 age cor dchol agelt50 $ Recall the data used in module 3 in the data file "dixonmassey." The general form for a confidence interval around the mean, if σ is unknown, isįor a two-sided 95% confidence interval, use the table of the t-distribution (found at the end of the section) to select the appropriate critical value of t for the two-sided α=0.05. We can also calculate a 95% confidence interval around the mean. Note: The shaded area is referred to as the critical region or rejection region. Using the significance level of 0.05, we reject the null hypothesis if |t| is greater than the critical value from a t-distribution with df = n-1. Using the significance level of 0.05, we reject the null hypothesis if z is greater than 1.96 or less than -1.96. Instructions: This calculator conducts a Chi-Square test for one population variance (. We choose an α = 0.05 significance level.Where μ 0 is a pre-specified value (in our case this would be 3,410 grams).
The population from which the data is sampled is normally distributed.For example we might know that the average birth weight for white babies in the US is 3,410 grams and wish to compare the average birth weight of a sample of black babies to this value. This is due to rounding error.A one sample test of means compares the mean of a sample to a pre-specified value and tests for a deviation from that value. We then calculate a test statistic \(Z_\text\). We’ll start by thinking about the rejection of a two-sided test. The rejection region in terms of the sample meanįor a given \(\alpha\) level threshold, all of these rejection regions are equivalent.The rejection region in terms of the test statistic.The rejection region in terms of the p-value.We can think about three different rejection regions for a Z-test: That said, sometimes it can be useful to think about when you reject a hypothesis test. Picking an arbitrary \(\alpha\) level rejection threshold and treating it as a gold standard is ridiculous, as evidenced by 60 years of statistical literature laden with warnings about hypothesis testing. If you do a hypothesis test, you should report the p-value, period. Preface: I am strongly opposed to make a dichotomous “reject/fail to reject” decision for hypothesis tests.


 0 kommentar(er)
0 kommentar(er)
